Wasserstein Distributional Robustness of Neural Networks
This post serves as an exposition of our recent work. Please refer to arXiv for a more detailed discussion and to GitHub for source codes.
Background
Deep neural networks have achieved great success in image classification tasks. We denote the feature of an image by $x$ and its class by $y$. A neural network $f_{\theta}$ takes $x$ as input and outputs the likelihood of each class the input could be. We denote $P$ as the data distribution. Then, we can write training of a neural network $f_{\theta}$ as finding the minimizer $\theta^{\star}$
\[\inf_{\theta} \E_{P}[J_{\theta}(x,y)] \leadsto \theta^{\star},\]where \(J_{\theta}(x,y)=L(f_{\theta}(x),y)\) for some loss function \(L\).
In the seminal paper

Classical literature on adversarial attacks, for example
Here, $\|\cdot\|$ is a norm on the feature space, which could be $l_2$, $l_{\infty}$, etc.
A key observation here is that,
\[\E_{P}\Bigl[\sup_{\|x-x'\|_s\leq \delta}J_{\theta}(x',y)\Bigr]=\sup_{\mathcal{W}_{\infty}(P,Q)\leq \delta}\E_{Q}\bigl[J_{\theta}(x,y)\bigr],\]where $\mathcal{W}_{\infty}$ is the $\infty$-Wasserstein distance induced by
\[\label{eqn-d} d((x_{1},y_{1}),(x_{2},y_{2}))=\|x_{1}-x_{2}\|+\infty\mathbf{1}_{\{y_{1}\neq y_{2}\}}.\]In this sense, finding the adversarial images is equivalent to finding the adversarial image distribution under the $\infty$-Wasserstein distance. This motivates us to investigate the distributional threat model and its associated adversarial attack, given by
\[\sup_{\mathcal{W}_{2}(P,Q)\leq \delta}\E_{Q}\bigl[J_{\theta}(x,y)\bigr].\]We quickly remark one main feature of distributional threat models. In contrast to the pointwise threat, the attacker has a greater flexibility and can perturb images close to the decision boundary only slightly while spending more of the attack budget on images farther away from the boundary. This makes the distributional adversarial attack more involved.
Such a W-DRO framework, while compelling theoretically, is often numerically intractable. We leverage the W-DRO sensitivity results
Setup
An image is interpreted as a tuple $(x,y)$ where the feature vector $x\in \mathcal{X}=[0,1]^{n}$ encodes the graphic information and $y\in\mathcal{Y}=\{1,\dots,m\}$ denotes the class, or tag, of the image. A distribution of labelled images corresponds to a probability measure $P$ on $\mathcal{X}\times\mathcal{Y}$. Under this setting $P$ could be the empirical measure on a given dataset or an inaccessible “true” distribution on the extended image space.
Let $(p,q)$ and $(r,s)$ be two pairs of conjugate indices with $1/p+1/q=1/r+1/s=1.$ As mentioned above, we equip $\mathcal{X}$ with $l_s$ norm and consider the Wasserstein distance $\mathcal{W}_p$ generated by $d$.
We write the neural network as a map $f_{\theta}:\mathcal{X}\to \mathbb{R}^{m}$. We denote $S$ the set of images equipped with their labels generated by $f_\theta$, i.e.,
\[S=\Bigl\{(x,y)\in \mathcal{X}\times\mathcal{Y}: \arg\max_{1\leq i\leq m} f_{\theta}(x)_{i}=\{y\}\Bigr\}.\]We denote the clean accuracy by \(A=\E_P[\mathbf{1}_S]\) and Wasserstein distributional adversarial accuracy by
\[A_{\delta}:=\inf_{\mathcal{W}_p(P,Q)\leq \delta}\E_Q[\mathbf{1}_S].\]Main Results
We always assume the following two assumptions hold.
(a) $0<Q(S)<1.$
(b) \( \mathcal{W}_{p}(Q(\cdot|S),P(\cdot|S))+\mathcal{W}_{p}(Q(\cdot|S^{c}),P(\cdot|S^{c}))= o(\delta), \) where \(S^{c}=(\mathcal{X}\times\mathcal{Y})\setminus S\) and the conditional distribution is given by $Q(E|S)=Q(E\cap S)/Q(S)$.
First Order Adversarial Attack
To propose WD adversarial attacks, we first introduce two important ingredients : sensitivity of W-DRO and rectified DLR loss.
We write
\[V(\delta)=\sup_{\mathcal{W}_{p}(P,Q)\leq \delta}\E_{Q}\bigl[J_{\theta}(x,y)\bigr].\]The following theorem is adapted from
(a) $V(\delta)=V(0)+\delta\Upsilon+o(\delta),$ where \begin{equation*} \Upsilon=\Bigl(\E_{P}\|\nabla_{x}J_{\theta}(x,y)\|_{r}^{q}\Bigr)^{1/q}. \end{equation*} (b) \(V(\delta)=\E_{Q_{\delta}}[J_{\theta}(x,y)]+o(\delta),\) where \begin{equation*} Q_{\delta}=\Bigl[(x,y)\mapsto \bigl(x+\delta h(\nabla_{x}J_{\theta}(x,y))\|\Upsilon^{-1}\nabla_{x}J_{\theta}(x,y)\|_{r}^{q-1},y\bigr)\Bigr]_{\#}P, \end{equation*} and \(h\) is uniquely determined by \(\langle h(x),x\rangle=\|x\|_{r}\).
The second result essentially says to maxize the loss, the perturbation given by
\[x\to x+\delta h(\nabla_{x}J_{\theta}(x,y))\|\Upsilon^{-1}\nabla_{x}J_{\theta}(x,y)\|_{r}^{q-1}\]is first-order optimal. Particularly, if we take $p=\infty$ and $q=\infty$, we retrieve Fast Gradient Descent Method (FGSM) mentioned above for pintwise threat models.
Under pointwise threat models, taking loss function $L$ as a combination of Cross Entropy (CE) loss and Difference of Logits Ratio (DLR) loss has been widely shown as an effective empirical attack, see
where we write \(z=(z_{1},\dots,z_{m})=f_{\theta}(x)\) for the output of a neural network, and \(z_{(1)}\geq\dots\geq z_{(m)}\) are the order statistics of \(z\). However, under distributional threat models, intuitively, an effective attack should perturb more aggressively images classified far from the decision boundary and leave the misclassified images unchanged. Consequently, neither CE loss nor DLR loss are appropriate. Instead, we propose to use Rectified DLR (ReDLR) loss as a candidate to employ distributional adversarial attacks, which is simply given by
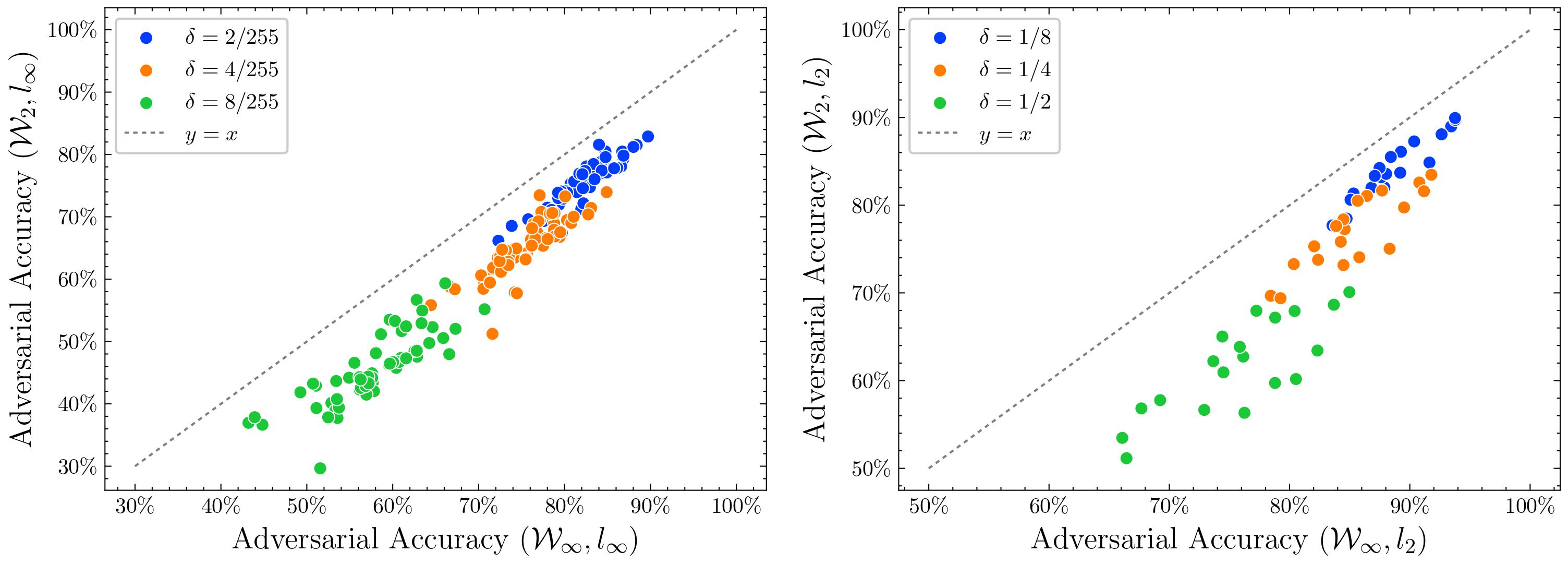
\[\mathop{\mathrm{ReDLR}}=-(\mathop{\mathrm{DLR}})^{-}.\]In the figure below, we compare the adversarial accuracy of robust networks on RobustBench
Asymptotically Certified Bound
We write \(\mathcal{R}_{\delta}:=A_{\delta}/A\) as a metric of robustness, and the adversarial loss condition on the misclassified images as
\[W(\delta)=\sup_{Q\in B_{\delta}(P)}\E_{Q}[J_{\theta}(x,y)|S^{c}].\]We note that an upper bound on $\mathcal{R}_\delta$ is given by any adversarial attack. In particular,
\[\mathcal{R}_\delta \leq \mathcal{R}^u_\delta:= Q_\delta(S)/A.\]Consequently, \(\mathcal{R}^l_{\delta}=\min\{\widetilde{\mathcal{R}}_\delta^l, \overline{\mathcal{R}}_{\delta}^l\}\) allows us to estimate the model robustness without performing any sophisticated adversarial attack. We plot our proposed bounds against the reference robust metric on CIFAR-100 and ImageNet datasets as below. For CIFAR-10 dataset, we refer to our paper. Notably, the bounds provided here is order of magnitude faster to compute than the reference value $\mathcal{R}_{\delta}$ by using AutoAttack


Out-of-Sample Performance
Our results on distributionally adversarial robustness translate into bounds for performance of the trained DNN on unseen data. We rely on the concentration inequality of empirical measures. Let us fix $1<p<n/2$. We assume the training set is i.i.d sampled from the true distribution $P$ with size $N$. Then the empirical measure of the training set $\widehat{P}$ is a random measure, and satisfies
\[\mathbb{P}(\mathcal{W}_p(\widehat{P},P)\geq \varepsilon)\leq K \exp(-KN\varepsilon^n),\]where $K$ is a constant depending on $p$ and $n$. Thank to W-DRO framework, such an estimate naturally yields the out-of-performance of neural networks under distributional threat models.
We remark that the above results are easily extended to the out-of-sample performance on the test set, via the triangle inequality.
Conclusion
Our work contributes to the understanding of robustness of DNN classifiers. It also offers a wider viewpoint on the question of robustness and naturally links the questions of adversarial attacks, out-of-sample performance, out-of-distribution performance and Knightian uncertainty. By introducing a first-order Adversarial Attack (AA) algorithm, we not only encompass existing methods like FGSM and PGD but also offer new insights into distributional threat models. We believe our research opens up many avenues for future work, especially training robust neural networks under distributional threat models.